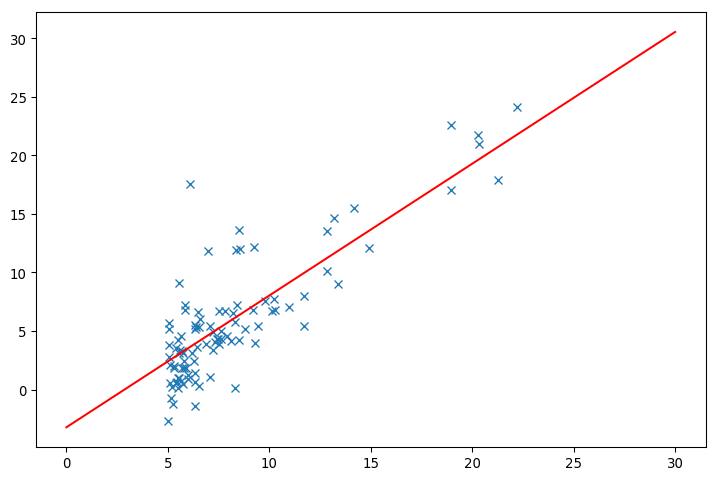
掐指一算,已经有三个月没有更新blog了。因为最近一直在学习机器学习的内容,所以没空也没有新鲜的技术值得写下来分享。还好经过一段时间的积累(学习线性代数和概率论),机器学习这块内容也算是入门了。这是机器学习的第一个习题,线性回归。用最直白的话来说,就是用函数去拟合数据分布,从而达到预测新数据的效果。需要的知识是矩阵的计算,最小二乘法以及求偏微分。
关键的公式只有两个:
那么最后需要确定的只剩下一个,我们希望用什么样的曲线去拟合样本,这个就需要经验和尝试了。这里的练习只需要用直线来拟合就足够了: \( h_\theta(x) = \theta^{T}x = \theta_{0}+\theta_{1}x_{1} \) .
# -*- coding: utf-8 -*- |